This is a free and brief translation of the article (original in English)
В previous article we already mentioned why Zilliqa requires a different protocol for consensus and why classical consensus Nakamoto (aka PoW) is not perfect.
The consensus protocol used in Zilliqa is called Practical Byzantine Fault Tolerance, or pBFT. This protocol has a number of advantages due to the low cost of its use - it does not require large amounts of energy to maintain system functionality and provides fast transaction verification.
However, the classic pBFT protocol developed by Castro and Liskov (original source) is only effective if consensus is carried out by a small group of, say, less than 50 nodes. The communication process between nodes quickly becomes a problem if consensus is achieved with, say, 600 nodes, which is a requirement in Zilliqa.
In this part, we want to discuss how high the interaction requirements are in the classic pBFT protocol, and how we reduce them using such a primitive technique as multi-signature.
Cost of data exchange in the pBFT protocol
This protocol obliges all honest nodes to agree on the state of the system. Thus, the nodes are in constant communication with each other. In the classic version of the protocol, each node interacts with all other nodes to exchange messages. If each node sends n number of messages, then the total required volume of information exchange will be approximately equal to n².
Cost of Authentication Messages
In addition, simply sending a message is not sufficient in a Byzantine network. For example, when node A receives a message from node B on an open Byzantine network, A must be sure that the message actually came from B and has not been modified in any way during transmission. Without such a guarantee, it is very difficult to verify the authenticity of a message and eliminate the possibility of substitution.
One solution to this problem is to generate a key that is kept secret between nodes A and B. This key can be used to generate a special tag that is assigned to each outgoing message. Since the key is known only to A and B, the tag can be generated exclusively by these nodes.
ImitationInsert (MAC) is a simple cryptography method that can generate such a tag. One of the possible ways to create a MAC is to use authentication code using a hash function.
Below is the method of using MAC by the sender and the recipient. The sender generates a tag using the message and the secret key and sends it to the recipient along with the message itself. The recipient also generates a tag and compares it with the one sent in the message. If both tags match, then the message was not modified in transit.
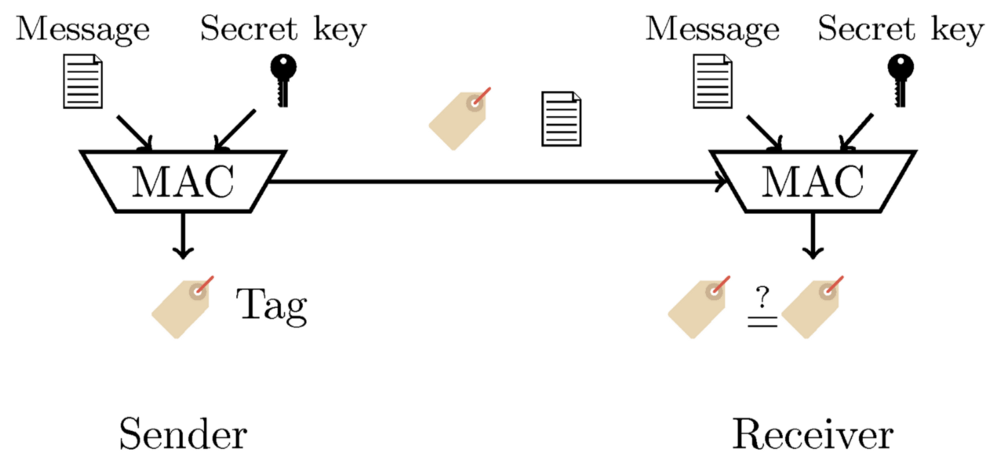
When using this technology, each pair of nodes must have your private key. Thus, if there are n number of nodes in the network, then the required number of keys will be as follows: n(n-1)/2.
Let's analyze the cost of data exchange when using a MAC a little deeper. Let's imagine that there are 4 nodes operating on the network: A, B, C, and D. Node A must send a message to the entire network, that is, B, C and D. Thus, A must generate 3 different tags with individual keys for B, C, and D. Now imagine that node A wants to use B as an intermediary to transfer tags from A to nodes C and D. In turn, B uses node C as an intermediary. Since B has already received an individual tag, it simply relays the remaining 2 tags, and so on. The total number of transmitted messages during such a “relay race” will be: 3+2+1+=6.
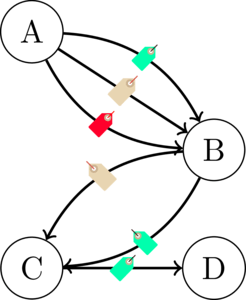
Three different tags generated by A are indicated by different colors. A sends 3 tag to node B, which sends the remaining 2 to node C. Finally, C redirects the last tag intended for D.
In a network with n nodes, the total number of messages (in the form of tags) will be: n + (n-1) + … + 1 = n (n+1)/ 2.
Public key cryptography as a means of increasing efficiency
MAC technology can be replaced with a digital signature, which will be used to verify the sender. Castro and Liskov did not use a digital signature in their work only because at that time computing MAC was much cheaper than creating a digital signature. Today, the cost of a digital signature is low.
Moreover, public key cryptography has its advantages. Let's return to the example discussed earlier with 4 nodes. Now let's imagine that A, B, C, and D have digital signatures. The node sends a message and adds its signature to it. The message is delivered to the nearest node, B. Please note that there is no need to create 3 signatures in this case, one signature is enough.
B receives the message and forwards it along with the signature A to node C, and so on. The total number of messages in this case will be 1+1+1=3.
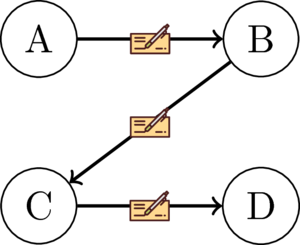
In a network with n nodes, the total number of messages will be as follows: 1 + 1 + 1 … (n-1) times = n-1.
The idea of replacing the MAC with a digital signature has already been put forward previously. The reduction in the number of messages sent is really great. Say, with n equal to 600, the number of messages sent is reduced from 180300 to 599.
Reducing the size of each message by using multi-signature.
Suppose we replace the MAC with a digital signature in the classic pBFT protocol. Now the question is: is there anything better than digital signatures? The answer is yes, even in this case there is room for improvement, and let's take a closer look at what exactly we can improve.
In the pBFT protocol, transactions are final, meaning that once a transaction is placed on the blockchain, it is committed. In such a system, invalid branches of the chain do not appear and, therefore, there is no need for confirmation. A transaction is considered confirmed based on the fact that, according to the pBFT protocol, each block must be signed by the vast majority of honest nodes. By signing, an honest node confirms that it has verified the contents of the block and all transactions in it are valid. In PoW consensus, a node generates a block and the rest of the network either accepts it or not, thus creating invalid branches of the chain.
In the system we are considering, each node signs a block and then forwards this block to other participants in the system. Each node adds its signature and, after some time, the block receives the vast majority of signatures from honest nodes. In the worst case, when every node (including suspicious ones) signs this block, the signature size will be equal to the value n. This is where multi-signature will optimize the system.
Simplified multi-signature operation scheme
With this principle of operation, the network must have n number of elements with signature rights (public and private keys); controller who verifies the signature; and an aggregator, which acts as a coordinator and “collects” the signatures sent by each element n. To simplify the example, we will assume that each node is honest and will be used to sign the message.
During the signature verification process, the controller also checks whether each element has signed the message correctly. If at least one signature is incorrect, then the entire verification is canceled.
Multisignature takes place in two stages. At first, each node sends its public key to the aggregator. All public keys are collected and a single public key is generated from them. Depending on the mathematical form of the keys, a single key can be generated by addition or multiplication.
For example, a single public key = public key_1 + public key_2 + … + public key_n.
At the second stage, the aggregator initiates an interactive protocol with each of the nodes. This protocol has three main phases of operation:
1. Commitment phase. In this phase, each node creates some arbitrary code. For those unfamiliar with the cryptographic bond scheme, a similar parallel can be drawn: Each node secretly rolls the dice, writes down the number on a piece of paper, places it in a box, locks it, and gives it to the aggregator. The aggregator should not be able to open the box.
2. Task construction phase. In this phase, the aggregator first collects all the commitments and creates a task using the public key and message. This task is then sent to each node. This is done to verify that each node actually knows the private key for the public key. This process is similar to how regular digital signatures work, where the signature is proof that the signer actually knows the private key.
3. Response phase. Each node sends a response to the task, which includes the use of a private key.
Thus, a final signature is formed, which can be verified using a single public key created at the first stage.

The size of such a signature is constant and does not depend on the number of signing nodes.
The node shaded in blue is an aggregator. H is a cryptographic hash function used to generate a task with message m. The pair R and S is a collective signature. R has the same size as R_i, and S has the same size as S_i. Generating a response is possible if you know the private key.
When the controller verifies the received signature, it does not control each node individually. The controller checks whether all nodes followed the protocol and confirmed knowledge of their private keys. Thus, an all-or-nothing decision is made.
Conclusion
Zilliqa uses several modern techniques that improve the efficiency of the classic pBFT protocol.
This article describes the use of a multi-signature protocol, which reduces the number of signatures from n to 1 and thus reduces the block size.
However, some questions remain open, and the most important one is what happens when only the vast majority of nodes sign a message, but not all nodes. Will the protocol still work? What changes should be made to the protocol?
In addition, are attacks possible when using a simplified version of the multisignature protocol?
There are two ways to answer these questions. The hard way is to read Zilliqa whitepaper. And an easy way is to ask questions in our communities.
Summary
Since the classic Nakamoto consensus is not ideal, companies are trying to develop more efficient consensus algorithms.
Zilliqa uses the Practical Byzantine Fault Tolerance, or pBFT, paradigm. This protocol is fast and does not require much energy, but its classic version has a bottleneck - achieving consensus with a large number of nodes in the network (Zilliqa requirements include the presence of at least 600 nodes).
This problem can be avoided by using imitative insertion (MAC), however, this method is outdated, and a digital signature is more relevant. At the same time, the multisignature method is the most modern today, as it allows you to effectively reduce the number of messages sent. This method requires improvement, since the operation of the protocol remains in question in a situation where not all nodes sign the message.


